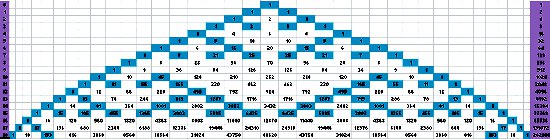
Pascal’s Triangle, Odd Numbers Highlighted
One of the great joys of being human is our incredible powers of pattern recognition. Our brain’s ability to manifest meaningful associations out of the complex morass of sensory stimuli perpetually assaulting us is a cognitive expertise into which computers are only just starting to venture successfully. It’s what allows us to recognize faces, raed wrdos wtih smrelcabd ltretes, identify with our fellow humans, and compartmentalize the sounds, tastes, and sights around us.
The number 11 has always been my favorite whole number. Ever since I was a kid, I appreciated the way the first nine multiples of 11 are numbers that mirror the tens and ones places (in a base-10 numbers system): {11, 22, 33, 44 … 77, 88, 99}.
You can figure out the result of eleven times any two-digit number by adding the tens and ones place of the two-digit number and placing it between the two digits. For example, eleven times my second favorite whole number:
| 69 X 11 = 759 |
| 6(6+9)9 |
| 6(15)9 |
| (Carry the one) |
| 759 |
You can also do something similar when multiplying eleven against a three-digit number.
Eleven is fun.
This year, the Gregorian Calendar has been filled with 11’s in its dates: 1/1/11, 1/11/11, 11/1/11, 11/11/11. Additionally, If you take the last two digits of the year you were born and add the age you will/have turned on your birthday this year, the result will be 111. For me, this is 73 + 38 = 111.
I previously blogged about eleven focusing on the trivia associated with the number, but I’ve come to understand that eleven is a wonderful number for all the patterns we can find in it, and nowhere do these patters become more clear than in Pascal’s Triangle:
Each row of Pascal’s Triangle sums to the set of exponents of two {1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024…}, and that’s interesting.
What’s more interesting? The digits of each row represent an exponent of eleven {11, 121, 1331, 14641, 161051, 1771561…}. It takes just a little bit of addition to see how this works for the rows with multiple-digit numbers. You have to think of each number as occupying a place value, like ones, tens, hundreds, thousands, etc. Then you carry the additional digits up to their appropriate place. For example, row six in Pascal’s Triangle is:
| 1 6 15 20 15 6 1 |
| 1 (6+1) (5+2) (0+1) (5) 6 1 |
| 1 7 7 1 5 6 1 |
| which is: |
| 116 |
So Pascal’s Triangle is a tower of powers of eleven, and the patterns within it continue. We can see the first set of diagonals going down the outsides of the triangle are all ones, and the second set of diagonals just inside this are all the natural numbers {1, 2, 3, 4, 5, 6, 7, 8, 9, 10…}. The third set of diagonals is Triangular Numbers, the number of building blocks needed to make triangles of increasing size:
Triangles One Through Six
The fourth set of diagonals are Tetrahedral Numbers, the number of building blocks needed to make tetrahedrons of increasing size.

Number Sets: Ones, Natural, Trangular, Tetrahedral, Pentatope
The fifth set of diagonals are Pentatope Numbers, which I don’t understand, but they sound like the number of building blocks needed to make 4-dimensional tetrahedron.
And the patterns continue! If we align all the numbers in Pascal’s Triangle up on one side, the diagonals add up to the Fibbonacci Set {1, 1, 2, 3, 5, 8 … 55, 89, etc, etc}, which relates back to my favorite irrational number Phi:
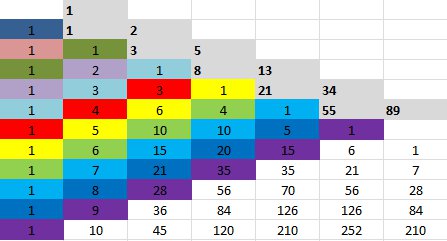
Fibbonacci Set in Pascal’s Triangle
(Diagonals colored, Sums Shaded Gray)
There is something fractaline about the conceptual patterns we are seeing in this numeric construction. There are triangles within triangles in the number sets. In fact, highlighting all the odd numbers within Pascal’s Triangle and zooming out far enough, we find an actual geometric fractal, a Sierpinski Triangle:
Powers of 10 Day celebrates the concept of exponential growth, a meditation on the size of our universe as we zoom in or out from our position within it. Powers of 11 Day seems like a good day to look at the patterns that emerge when we zoom out to look down on the big picture. There are patterns within patterns when we line up the powers of eleven in this way, beautiful symmetry, dimensions beyond our three, and geometry that echoes across the function. Our brains evolved to find patterns everywhere in the world, and this mathematical object is perfect for enjoying the immense potential of this natural cognitive proclivity within us.
Further Reading
The images of Pascals Triangle that I composed myself for this post were put together in Microsoft Excel, and you can download the spreadsheet if you’d like to play with the numbers yourself.
Special thanks to Math Forum for the best, most simplest page on the web exploring Pascal’s Triangle and the powers of 11.
In hacker slang, “Elite” is transformed into “leet” which is transformed into “1337” which is transformed to “1331” which is transformed into “leel” which is the highest form of elite. 1331 is 11 to the third power.
I recently discovered this Chinese version of the triangle, Yang Hui’s triangle from the 12th century, but the earliest references to the triangle are from India in 2nd century BC:

Yang Hui’s triangle


