Relating Thermodynamic Entropy to Information Entropy with Maxwell’s Demon

Brownian motion, the natural vibrations of atoms not at an absolute zero temperature, has long been the strategic key for anyone looking for a way to achieve the holy grail of reversing the Second Law of Thermodynamics, which states that a closed system will always move toward a state of increasing disorder. I previously covered Richard Feynman’s Brownian Ratchet, which harnessed the power of Brownian motion to turn a rotor, and, as Feynman explains, wouldn’t work because the device would need to be so small that it would vibrate apart from the Brownian motion of its own molecules. “There’s no such thing as a free lunch,” to quote the old adage, or “You can’t stuff the mushroom cloud back into the shiny uranium sphere,” to quote Robert Heinlein, or “Things fall apart. It’s scientific,” to quote the Talking Heads.

Illustration of a Particle Rising in Potential Energy through Information Alone
Credit: Nature Physics, doi:10.1038/nphys1821

Last week, a paper published in Nature Physics, Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality, described an experiment where information was converted into energy by exploiting Brownian motion. It involved using the vibrations of an atom and observations of its changing position to let it naturally work its way up a sine wave, increasing its potential energy, which could, theoretically, be used to perform work when it vibrates back down the wave. It was a real-world demonstration of another thought experiment that challenged the Second Law. In 1867 Scottish physicist James Clerk Maxwell crafted a scenario whereby Brownian motion could be exploited to sort atoms according to their energy states, which later became known as Maxwell’s Demon¹, an apparent violation of the second law:

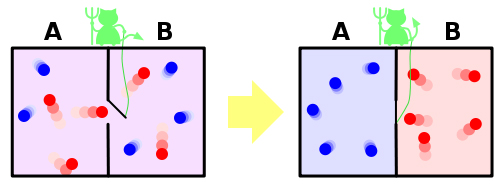
… if we conceive of a being whose faculties are so sharpened that he can follow every molecule in its course, such a being, whose attributes are as essentially finite as our own, would be able to do what is impossible to us. For we have seen that molecules in a vessel full of air at uniform temperature are moving with velocities by no means uniform, though the mean velocity of any great number of them, arbitrarily selected, is almost exactly uniform. Now let us suppose that such a vessel is divided into two portions, A and B, by a division in which there is a small hole, and that a being, who can see the individual molecules, opens and closes this hole, so as to allow only the swifter molecules to pass from A to B, and only the slower molecules to pass from B to A. He will thus, without expenditure of work, raise the temperature of B and lower that of A, in contradiction to the second law of thermodynamics….

In other words, something like the following diagram (or you can play the role of Maxwell’s demon in this online simulation):

Maxwell’s Demon
Credit: Htkym

I don’t like this description because it’s too elaborate, sounds as if it’s invoking magic with the fantastical demon, and begs too many questions about the hypothetical mechanism by which the barrier will be opened and closed. How will that work without spending energy?

The answer: fugetabout it. There are lots of possible mechanisms, all of which will cost varying degrees of energy to function², but that’s immaterial to what this situation is illustrating. The gate is not acting on the atoms to sort them, the atoms’ natural Brownian motion is moving them about and the well-timed use of the gate simply captures them in a state of less entropy and prevents them from returning to a state of increased entropy.

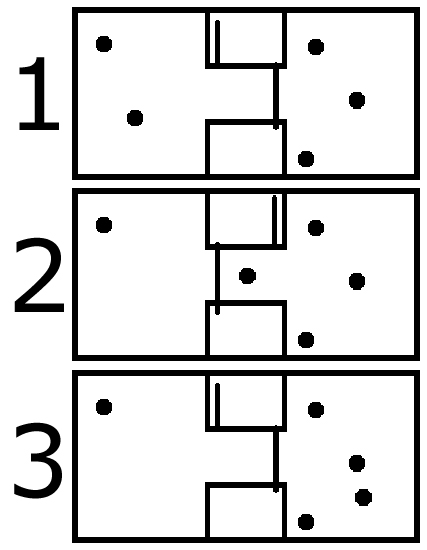
Take this much simpler example, where the gate is closed only once at a point when there are no molecules in a portion of a vial:

A Simple Tube Gate Increases the Air Pressure
Credit: Eric H. Neilsen

The entropy of the gas in the vial has been reduced, storing potential energy in the form of air pressure. If the amount of work into which that air pressure can be transformed exceeds the entropy generated in closing the gate, a distinct possibility, then it appears we have violated the second law. So where did the missing entropy go?

According to Leó Szilárd in 1929, and later reaffirmed by Léon Brillouin, the entropy was generated in the creation of information. An observer had to logically recognize the opportunity to strategically drop the gate, which meant they had to generate entropy pinning down the bits, the ones and zeroes, for that information.

How much energy? In Maxwell’s example, the demon has to know the velocity and position of the atoms in the box. That’s a lot of information to quantify. In the simpler example, the demon would still need to know the positions of the atoms to know where to drop the gate, also a lot of information. We need to come up with the simplest scenario where the least amount of information is needed to reduce the entropy in the box:

One Bit of Information Needed to Reduce the Entropy
Credit: Eric H. Neilsen

In this design, we have two trap doors and a chamber between them. We are trying to get the atoms in the right container into the left container to increase the air pressure and potential energy in the system. We have a simple computer program controlling the two gates that goes like this (in pseudocode):


If the number of atoms in the chamber is greater than 0:
Open left gate, Close right gate
Else:
Close left gate, open right gate


In this setup, it only takes one bit of information to decrease the entropy in the system, as simple as it can get, and the energy required to set a single bit is k T ln2, as explained here:

John von Neumann, in a 1949 lecture, set the minimum price of “an elementary act of information” at kT ln 2. In this formula k is Boltzmann’s constant, which is the conversion factor for expressing temperature in energy units; its numerical value is 1.4 x 10-23 joules per kelvin. T is the absolute temperature, and ln 2 is the natural logarithm of 2, a number that appears here because it corresponds to one bit of information—the amount of information needed to distinguish between two equally likely alternatives. At room temperature (300 kelvins), kT ln 2 works out to about 3 x 10-21 joule, or 3 zeptojoules. This is a minuscule amount of energy; Ralph C. Merkle of the Georgia Institute of Technology estimates that it is the average kinetic energy of a single air molecule at room temperature. [emphasis mine]

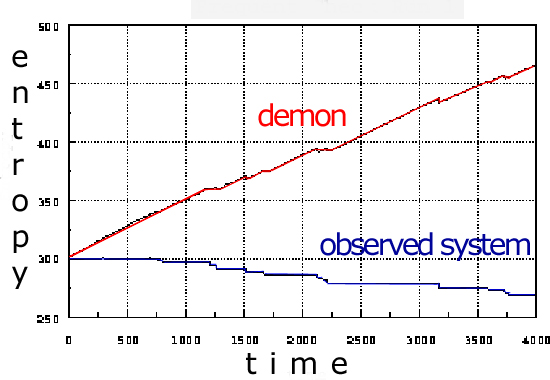
So the energy necessary to set a bit would be the same as the average energy of an atom at room temperature. So the entropy reduced from the system with each atom sorted is equal to that of the entropy generated in the demon for each bit of memory needed to recognize that the switch should be flipped. Case closed? Not quite. The total entropy must increase in the system for the Second Law to hold; the syntropy (reduction in entropy) and entropy cannot be equal.

So where is the remaining entropy? The answer, it appears, is that it is bound up in the information. At some point we have to release these bits from memory to make space for new bits. Erasing bits also takes energy. According to Landauer’s principle, after Rolf Landauer of IBM in 1961, it costs the same amount of energy as it took to set it. In other words, the set bit has potential entropy stored within it, which gets released when the information is released, a final cost of two times k T ln2, meaning the entropy generated within the demon is twice what it removes from the system it is manipulating.

And there will be a need to free memory. Note that in this example, we are only considering the cost of observing the system once against the gain of increasing the air pressure by one atom. In reality, we would also need to consider the frequency of observations the demon would have to make, checking the system periodically to determine whether there’s an atom to let through or not. The demon will quickly experience diminishing returns, and the amount of entropy generated in memory consumption will outstrip the entropy removed from the observed system.

Demon Entropy vs Entropy Removed
Credit: Eric H. Neilsen

I’ve given this topic a painfully overly simplistic treatment that doesn’t take into account the myriad of other thought experiments on the subject, the possibility of reversible computing, or loads of other deeply philosophical, mathematically-challenging errata, but it should provide deeper insights into what the University of Tokyo researchers accomplished: allowing Brownian motion to give a particle the chance of moving up a sine wave, recognizing when it did so using information, and moving the gate to prevent it from vibrating back down the steps, transforming information into potential energy. While I have covered the most extreme hypothetical means of reducing the entropy generated to do this, they did this at the cost of energy to run the apparatus for observing the particle, the electric field to prevent it from rattling down the wave, and to power the researchers operating it. In comparison to the amount of potential energy added to this single particle, the entropy generated was gargantuan.

Reference:

Toyabe, S., Sagawa, T., Ueda, M., Muneyuki, E., & Sano, M. (2010). Experimental demonstration of information-to-energy conversion and validation of the generalized Jarzynski equality Nature Physics DOI: 10.1038/nphys1821

¹ Note: the term “demon” here is simply meant to indicate an agent performing a service, similar to the way the term is used in Computer Science for certain software processes (Fox News won the stupidest headline award on this one with “Scientists Convert Information into “Demonic” Energy, which led to a few interesting comments by Christians on the article).

² My favorite barrier would be one that uses a pendulum to open and close. When the pendulum is at one of the apexes of its swing, it is caught and a little bit of energy is expended to raise it to the height it was at initially

Further Reading: