Here I thought I was so cool coming up with “Somma’s Stochaistic,” the idea that science is inversely proportional to BS:
 Somma’s Stochaistic |
Now I find out somebody else all ready came up with it and expressed it my more elegantly in something called: Bayesian Probability. The equation for this concept looks like this:
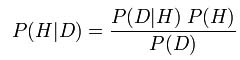 Bayesian Probability |
Where:
- H is a hypothesis
- D is the data
- P(H) is the probability that H is correct before the data D was seen.
- P(D | H) is the conditional probability of seeing the data given that the hypothesis is true.
- P(D) is the marginal probability of D.
- P(H | D) is the probability that the hypothesis is true, given the data and the previous state of belief about the hypothesis.
Interestingly enough, the above equation simplifies to this:
|
Bayesian Probability Simplified |
Stated simply: The probability of being wrong is inversely proportional to the amount of data available.
Paraphrased simply: Science is inversely proportional to BS.