Marsday Book Review: Sacred Geometry

The Negatives

Sacred Geometry Deciphering the Code

Pursuant to my interest in the beauty of mathematical ideas, I decided to pick up a copy of Stephen Skinner’s book, Sacred Geometry, which surveys the beauty and synchronicities of whole numbers and geometric concepts. This is a beautify, however somewhat flawed book, and I’ve decided to break my review of it up into two posts highlighting its negative and positive aspects. I like to get the negatives out of the way up front, and leave off with positives. So…

Two Glaring Goof Ups

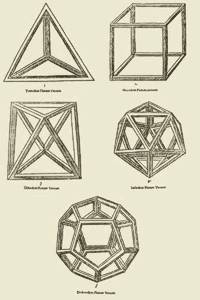Da Vinci’s Drawings of the Platonic Solids (Tetrahedron, Hexahedron, Octahedron, Icosahedron, Dodecahedron)

In the section on the five platonic solids, Skinner notes that the hexahedron (earth) and octahedron (air) are a pair, meaning it’s possible to create one from the other by connecting the vertices to the centers of the faces. Correct, but then he writes that the icosahedron (water) and tetrahedron (fire) are also a pair in this sense, and the dodecahedron (ether) is a pair unto itself; therefore, poetically, ether comes from ether.

Wrong. It’s the icosahedron and dodecahedron that are a pair, each forming the other. I know this because, for a brief phase in my life, I was spending my leisure time getting schnookered and playing with Zome Tools, and have built this association myself. It is the tetrahedron that makes itself; therefore, not quite so poetically, fire comes from fire.

Skinner, like most skips–or doesn’t know about–what I think is the most fascinating aspect of the icosohedron platonic solid: the fact that it is possible to generate three golden rectangles inside it by connecting the vertices. I am so enchanted by this fact, that I keep a ZomeTool model of an icosahedron with the interlaced golden rectangles on my desk at work. It serves as a warning to my geeky coworkers that this desk is my territory:

Ryan’s Icosahedron With Golden Rectangles Highlighted

Now, as Professor Bender will instruct, ignore the cross lines in the figure, but note the rectangle, which has proportions according to the golden rectangle. Now imagine Dr. Bender rotating the object 180-degrees along the horizontal axis, and the horizontal line will reveal another golden rectangle. A 180-degree twist on the vertical axis, and the vertical line will reveal a golden rectangle. Doesn’t that just make your eyes glaze over with indifference???

Me too. Here’s some good pictures of what I’m talking about. Let’s move on.

When discussing prime numbers, Skinner cites Peter Plichta’s Prime Number Circle, which is titled “Prime Number Cross” in the reference I found, but this is an obscure mathematical construction. I suspect his reasoning for using it is Plichta’s focus on figuring out “God’s Secret Formula” from primes, which he didn’t… or maybe he did, and god killed him to keep it a secret. : )

A much more well-known and, to my mind, interesting construct is the Ulam Spiral and the variant Sacks Spiral. Both of these illustrate in much more dramatic detail the concept of primes “regular irregularity,” as Skinner is attempting to illustrate them.

These last two are not errors, but the omissions do make me wonder what else I was missing out on that the author didn’t know about, or didn’t fit in with the theme of his book?

Tomorrow I’ll talk about what I liked in this book.

The Positives

Sacred Geometry Deciphering the Code

Enchantments

Reading this book took some time. Every two-page spread explores a single concept, and I found myself meditating on the subject matter with every turn of the page, trying to master its concepts. In a few places, I was forced to move on, but, for the most part, Skinner gives the introductory reader everything they should need to grasp the material.

I’m a collector of Phi trivia, and this book did a great job of pointing me to many unfamiliar facts about this golden number and clarifying facts I knew, but didn’t understand.

For instance, did you know the pentagram’s five points are golden triangles? I didn’t. It’s also possible to construct golden triangles inside a pentagon. Using repeating golden triangles, it’s possible to create a sort of pentagram-fractal.

ZomeTool’s connector balls are small rhombicosidodecahedrons

I found in the book’s section on the 13 Archimedean solids (which I had never heard of before (to my delight)), that the connector-balls in the zome construction sets are actually small rhombicosidodecahedrons.

Euclid’s Elements (with cool interactive illustrations, however questionably appropriate),

In other places, Skinner’s observations are interesting, but it feels as though he is stretching to make the connection. Like when he points out that there are 81 stable elements on Earth, and the letters in the Gnostic name for god, IAO, add up to 81, and 81 is an important number on the greek lambda, which is based on the Pythagorean tetractys, which is related to the musical scale.

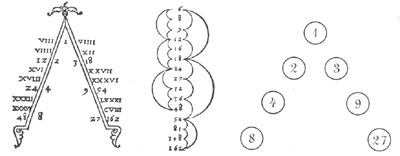Greek Lambda, Musical Scales, and Tetractys (It all fits together somehow!)

Reading this actually makes me a little embarrassed about my interest in phi, because it shows that, if you look hard enough, you’ll find connections and synchronicities in everything.

I think this grasping for meaning in every little thing is what makes the book’s final chapters, which explore the mathematical basis of ancient architectures and works of art, the least interesting. So Leonardo Da Vinci, St. Paul’s Cathedral, and the Parthenon all use “sacred” proportions in their works (note the scare-quotes). All this means is that the humans building them put what they considered sacred into their art and architecture. This is not as fascinating as these numbers occurring the DNA’s double helix, jellyfish colonies, astronomy, snowflakes, and water turbulence, which the book covers in earlier chapters.

Overall, this is a very pretty book. Only time will tell if it survives on my very selective bookshelf over the years, but for right now, I really enjoy flipping through its pages and immersing myself in mathematical ideas as they are expressed in human constructs, nature, geometric figures, and abstract concepts.