What is Chaos Theory?

Chaos theory deals with the ultimately unpredictable nature of our universe. The Principles of Chaos Theory were discovered by a meteorologist named Edward Lorenze, who was working on the problem of predicting weather patterns in 1960. One day in 1961 he ran a mathematical sequence through a computer that he had run previously.
When He returned, he found a set of results wildly different from his originals. He eventually traced this difference in outcomes to the number he had entered off of the printout, which had been calculated to only 3 decimal places to save paper. The original sequence had run on the number .506127, he had only entered the number .506.
The conventional wisdom of the time stated that such a miniscule difference in figures should have produced very similar results. Being able to measure something to the third decimal place was quite an accomplishment. The fact that a difference of .000127 between the initial and subsequent conditions could cause such drastically different results called the predictability of complex systems into question. Weather, population growth, the orbits of planets, all of these systems were proven ultimately unpredictable.
The Chaos theory metaphor is the flapping of a butterfly’s wings in Central Park creating a monsoon in Asia. The three decimal places represent the flapping of a butterfly’s wings, and the monsoon is the unpredictable result of leaving the butterfly out of the equation.
Now consider some numbers that are mathematical constants in so many of our equations:
0.000 000 000 000 000 000 000 000 006 626
Planck’s Constant (h)
The Pattern of Chaos, Infinite Regression
Fractals
Fractals are objects that display self-similarity at various scales. Magnifying a fractal reveals small-scale details similar to the large-scale characteristics. Like Pi or Phi, fractals are infinite geometric expressions that do not repeat as we explore them, but exhibit different expressions of their basic form throughout.
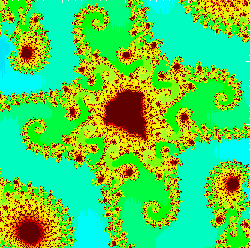
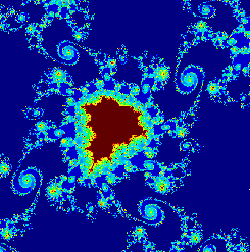
The Mandelbrot Set
This is the set of points in the complex c-plane that do not go to infinity when iterating zn+1=zn2+c starting with z=0. The set is famous for its relative simplicity, but startlingly complex expressions:
 |
 |
 |
 |
 |
 |
The Julia Set
When we leave the variable c fixed through our iterations of the equation, we achieve a different fractal. Some expressions of the Julia set are known as “Dragon Fractals”.
 |
 |
 |
 |
 |
Artists, such as Linda Bucklin, have begun constructing artwork out of chaos theory. Here are two examples of her work with fractals:
 |
 |
Beyond…
Nature’s Fractals

The Pattern of a Snowflake in the Koch Curve
Henry David Thoreau, in his classic text “Walden”, recognized the repeating patterns of the natural world:
“When the frost comes out in the spring, and even in a thawing day in the winter, the sand begins to flow down the slopes like lava, sometimes bursting out through the snow and overflowing it where no sand was to be seen before. Innumerable little streams overlap and interlace one with another, exhibiting a sort of hybrid product, which obeys half way the law of currents, and half way that of vegetation. As it flows it takes the forms of sappy leaves or vines, making heaps of pulpy sprays a foot or more in depth, and resembling, as you look down on them, the laciniated, lobed, and imbricated thalluses of some lichens; or you are reminded of coral, of leopard’s paws or birds’ feet, of brains or lungs or bowels, and excrements of all kinds.”
 |
 |
 |
Pattern repeats: Geometric Design, a Pinecone, a Sunflower
Dirt, streams, the branches of trees, the veins of our circulatory system, these are natural patterns that repeat and mimic one another. We can see a repetitive pattern in the suns circling galaxies, planets circling suns, and electrons circling atoms. For some of these patterns, like the growth of trees and the patterns of animal hides, we have decoded the mathematical formulas to express them. Other patterns, like the macro cosmos of our universe, are impossible to define.
The Fibonacci Set
{1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,…}
Each number in this set is equal to the sum of the two numbers preceding it. The set is used to predict population growth, the branching of plant stems, and even the radiation of cactus needles. An interesting phenomenon occurs when we divide each number in the set by its predecessor:
| 1 | / | 1 | = 1 |
| 2 | / | 1 | = 2 |
| 3 | / | 2 | = 1.5 |
| 5 | / | 3 | = 1.6666667 |
| 8 | / | 5 | = 1.6 |
| 12 | / | 8 | = 1.625 |
| 21 | / | 13 | = 1.6153846 |
| 34 | / | 21 | = 1.6190476 |
We get closer and closer to the number Phi (1.618033988…), but never reach it precisely. There is a sort of romantic poetry in this ratio, which we find expressed in so many natural ways in our world.
 |
 |
Pattern repeats: A fractal, a Cactus
Reality’s Infinite Mystery
Fractals, Pi, Chaos Theory are all mathematical proofs for the infinite nature of certain aspects of our universe. You would spend an infinite amount of time chasing down the secrets of Pi. Even with an ocean of numbers behind you, discovered and relegated to the known, the unknown next number still lies just over the horizon, and like the horizon, you may chase it endlessly, but never reach it.
There are two attitudes we may take to this revelation. We can look at existence as hopeless, a futile struggle to attain infinity. Such pessimism is an easy rationalization for the lazy mind, which seeks stasis and abhors the efforts that growth demands.
The alternative is to see this as a voyage of infinite discovery, with no end in sight, or even mathematically possible.

Further Reading:
Stewart, Ian, Does God Play Dice? The Mathematics of Chaos, Penguin Books Ltd, Harmondsworth, Middlesex, 1989.

